kaolin.ops.spc

Structured Point Clouds

Structured Point Clouds (SPC) is a sparse octree-based representation that is useful to organize and compress 3D geometrically sparse information. They are also known as sparse voxelgrids, quantized point clouds, and voxelized point clouds.

Kaolin supports a number of operations to work with SPCs, including efficient ray-tracing and convolutions.

The SPC data structure is very general. In the SPC data structure, octrees provide a way to store and efficiently retrieve coordinates of points at different levels of the octree hierarchy. It is also possible to associate features to these coordinates using point ordering in memory. Below we detail the low-level representations that comprise SPCs and allow corresponding efficient operations. We also provide a convenience container for these low-level attributes.

Some of the conventions are also defined in Neural Geometric Level of Detail: Real-time Rendering with Implicit 3D Surfaces which uses SPC as an internal representation.

Warning

Structured Point Clouds internal layout and structure is still experimental and may be modified in the future.

Octree

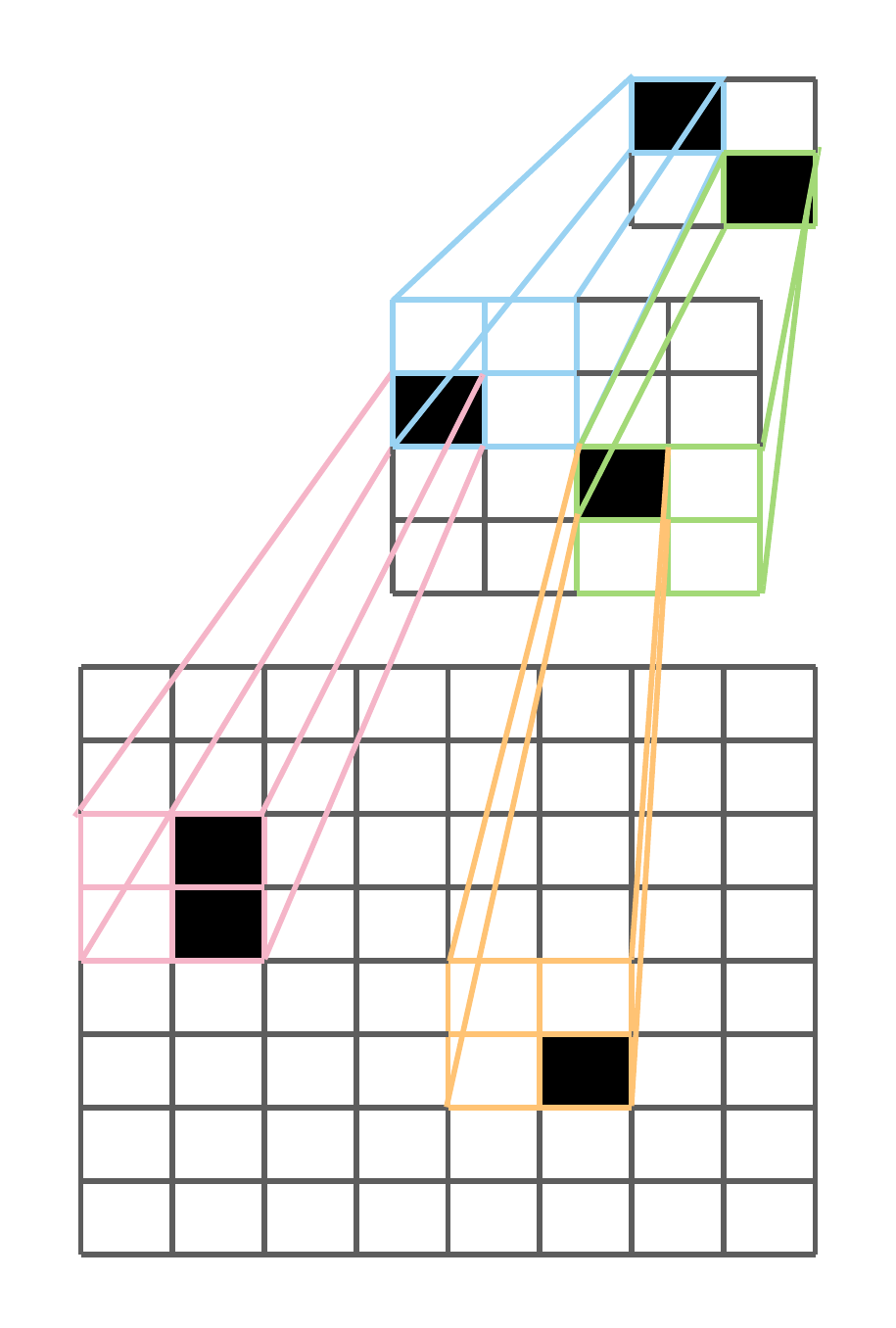
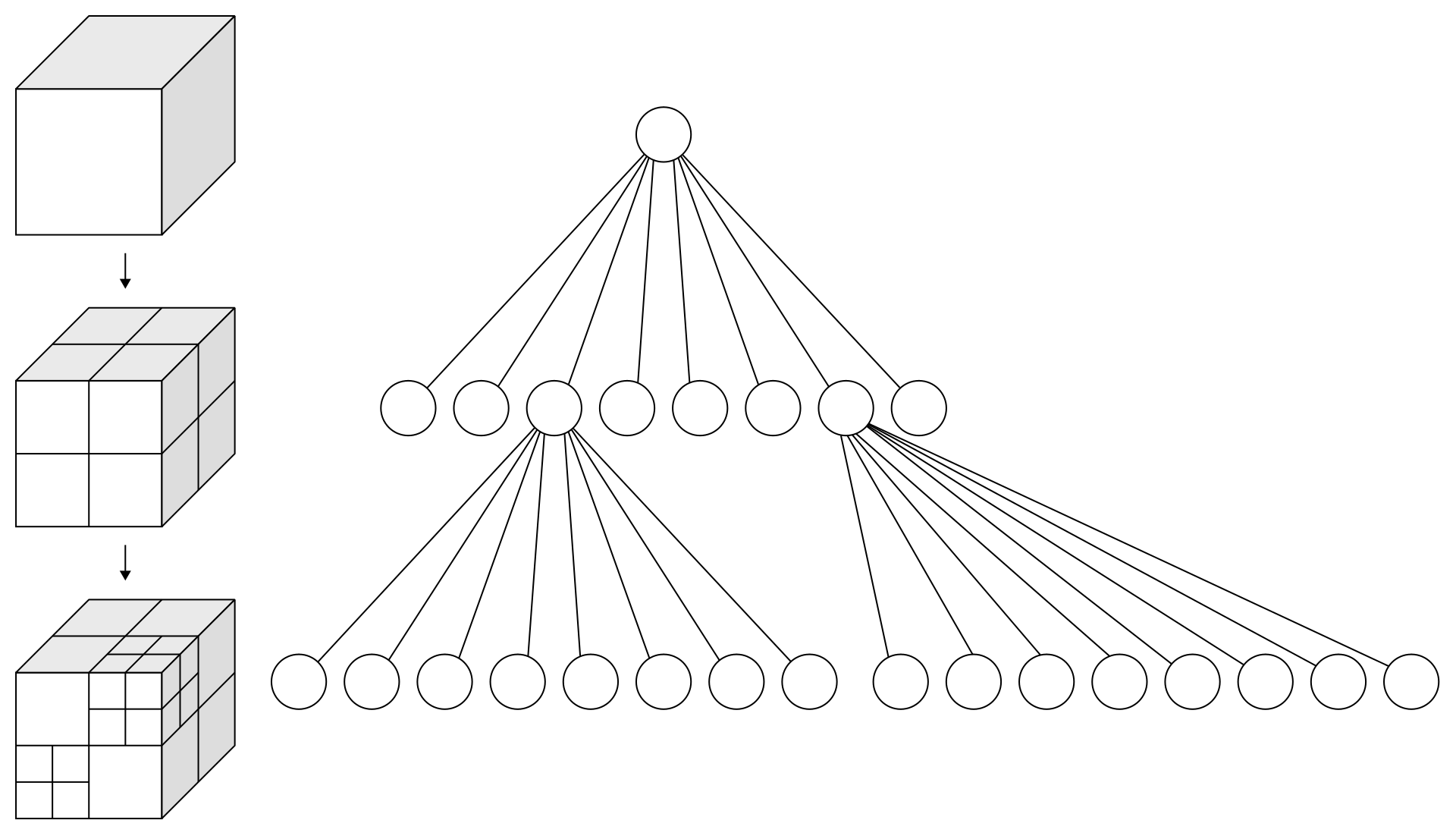
Core to SPC is the octree, a tree data structure where each node have up to 8 childrens. We use this structure to do a recursive three-dimensional space partitioning, i.e: each node represents a partitioning of its 3D space (partition) of \((2, 2, 2)\). The octree then contains the information necessary to find the sparse coordinates.

In SPC, a batch of octrees is represented as a tensor of bytes. Each bit in the byte array octrees represents the binary occupancy of an octree bit sorted in Morton Order. The Morton order is a type of space-filling curve which gives a deterministic ordering of integer coordinates on a 3D grid. That is, for a given non-negative 1D integer coordinate, there exists a bijective mapping to 3D integer coordinates.

Since a byte is a collection of 8 bits, a single byte octrees[i] represents an octree node where each bit indicate the binary occupancy of a child node / partition as depicted below:

../_images/octants.png

For each octree, the nodes / bytes are following breadth-first-search order (with Morton order for childrens order), and the octree bytes are then Packed to form octrees. This ordering allows efficient tree access without having to explicilty store indirection pointers.

An octree 3D partitioning

Credit: https://en.wikipedia.org/wiki/Octree

The binary occupancy values in the bits of octrees implicitly encode position data due to the bijective mapping from Morton codes to 3D integer coordinates. However, to provide users a more straight forward interface to work with these octrees, SPC provides auxilary information such as points which is a Packed tensor of 3D coordinates. Refer to the Related attributes section for more details.

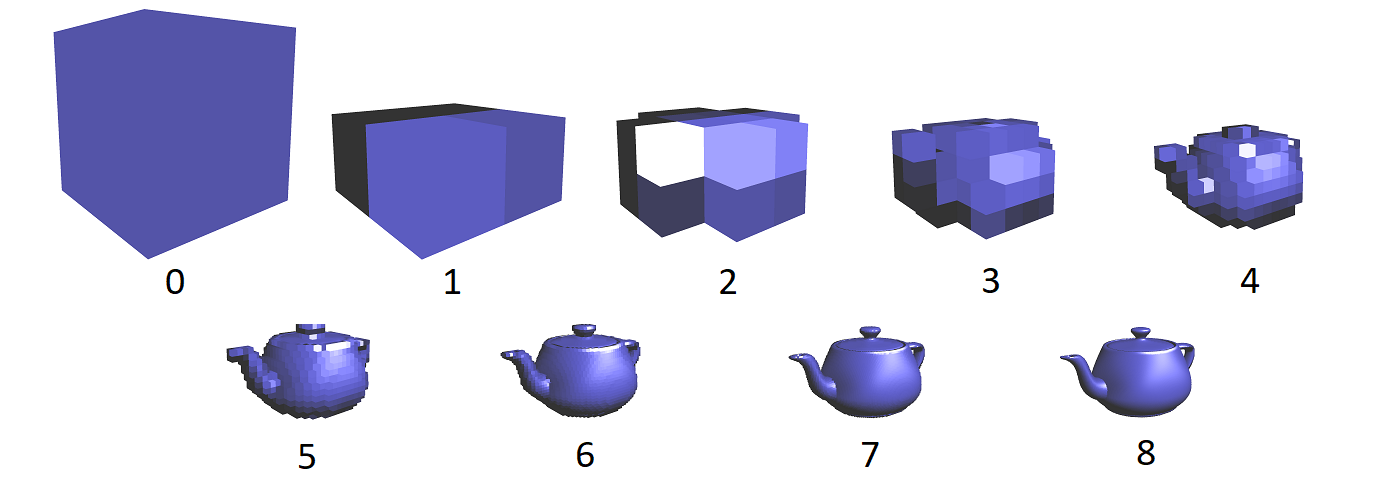
Currently SPCs are primarily used to represent 3D surfaces, and so all the leaves are at the same level (depth). This allow very efficient processing on GPU, with custom CUDA kernels, for ray-tracing and convolution.

The structure contains finer details as you go deeper in to the tree. Below are the Levels 0 through 8 of a SPC teapot model:

../_images/spcTeapot.png

Additional Feature Data

The nodes of the octrees can contain information beyond just the 3D coordinates of the nodes, such as RGB color, normals, feature maps, or even differentiable activation maps processed by a convolution.

We follow a Structure of Arrays approach to store additional data for maximum user extensibility. Currently the features would be tensors of shape \((\text{num_nodes}, \text{feature_dim})\) with num_nodes being the number of nodes at a specific level of the octrees, and feature_dim the dimension of the feature set (for instance 3 for RGB color). Users can freely define their own feature data to be stored alongside SPC.

Conversions

Structured point clouds can be derived from multiple sources. Using kaolin.ops.conversions.trianglemeshes_to_spcs() will convert batched triangle mesh models into octrees. We can also construct octrees from unstructured point cloud data, from sparse voxelgrids or from the level set of an implicit function \(f(x, y, z)\).

Convolutions

We provide several sparse convolution layers for structured point clouds. Convolutions are characterized by the size of the input and output channels, an array of kernel_vectors, and possibly the number of levels to jump, i.e., the difference in input and output levels.

An example of how to create a \(3 \times 3 \times 3\) kernel follows:

>>> vectors = []
>>> for i in range(-1, 2):
>>>     for j in range(-1, 2):
>>>         for k in range(-1, 2):
>>>             vectors.append([i, j, k])
>>> Kvec = torch.tensor(vectors, dtype=torch.short, device=device)
>>> Kvec
tensor([[-1, -1, -1],
        [-1, -1,  0],
        [-1, -1,  1],
        ...
        ...
        [ 1,  1, -1],
        [ 1,  1,  0],
        [ 1,  1,  1]], device='cuda:0', dtype=torch.int16)

The kernel vectors determine the shape of the convolution kernel. Each kernel vector is added to the position of a point to determine the coordinates of points whose corresponding input data is needed for the operation. We formalize this notion using the following neighbor function:

\[n(i,k) = \text{ID}\left(P_i+\overrightarrow{K}_k\right)\]

that returns the index of the point within the same level found by adding kernel vector \(\overrightarrow{K}_k\) to point \(P_i\). Given the sparse nature of SPC data, it may be the case that no such point exists. In such cases, \(n(i,k)\) will return an invalid value, and data accesses will be treated like zero padding.

Transposed convolutions are defined by the transposed neighbor function

\[n^T(i,k) = \text{ID}\left(P_i-\overrightarrow{K}_k\right)\]

The value jump is used to indicate the difference in levels between the iput features and the output features. For convolutions, this is the number of levels to downsample; while for transposed convolutions, jump is the number of levels to upsample. The value of jump must be positive, and may not go beyond the highest level of the octree.

Examples

You can create octrees from sparse feature_grids (of shape \((\text{batch_size}, \text{feature_dim}, \text{height}, \text{width}, \text{depth})\)):

>>> octrees, lengths, features = kaolin.ops.spc.feature_grids_to_spc(features_grids)

or from point cloud (of shape \((\text{num_points, 3})\)):

>>> qpc = kaolin.ops.spc.quantize_points(pc, level)
>>> octree = kaolin.ops.spc.unbatched_points_to_octree(qpc, level)

To use convolution, you can use the functional or the torch.nn.Module version like torch.nn.functional.conv3d and torch.nn.Conv3d:

>>> max_level, pyramids, exsum = kaolin.ops.spc.scan_octrees(octrees, lengths)
>>> point_hierarchies = kaolin.ops.spc.generate_points(octrees, pyramids, exsum)
>>> kernel_vectors = torch.tensor([[0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 1, 1],
                                   [1, 0, 0], [1, 0, 1], [1, 1, 0], [1, 1, 1]],
                                  dtype=torch.ShortTensor, device='cuda')
>>> conv = kaolin.ops.spc.Conv3d(in_channels, out_channels, kernel_vectors, jump=1, bias=True).cuda()
>>> # With functional
>>> out_features, out_level = kaolin.ops.spc.conv3d(octrees, point_hierarchies, level, pyramids,
...                                                 exsum, coalescent_features, weight,
...                                                 kernel_vectors, jump, bias)
>>> # With nn.Module and container class
>>> input_spc = kaolin.rep.Spc(octrees, lengths)
>>> conv
>>> out_features, out_level = kaolin.ops.spc.conv_transpose3d(
...     **input_spc.to_dict(), input=out_features, level=level,
...     weight=weight, kernel_vectors=kernel_vectors, jump=jump, bias=bias)

To apply ray tracing we currently only support non-batched version, for instance here with RGB values as per point features:

>>> max_level, pyramids, exsum = kaolin.ops.spc.scan_octrees(
...     octree, torch.tensor([len(octree)], dtype=torch.int32, device='cuda')
>>> point_hierarchy = kaolin.ops.spc.generate_points(octrees, pyramids, exsum)
>>> nuggets = kaolin.render.spc.unbatched_raytrace(octree, point_hierarchy, pyramids[0], exsum,
...                                                origin, direction, max_level)
>>> first_hits_mask = kaolin.render.spc.mark_first_hit(nuggets)
>>> first_hits_nuggets = nuggets[first_hits_mask].long()
>>> first_hits_rgb = rgb[first_hits_nuggets[:, 1] - pyramids[max_level - 2]]

API

class kaolin.ops.spc.Conv3d(in_channels, out_channels, kernel_vectors, jump=0, bias=True)

Bases: torch.nn.modules.module.Module

Convolution layer for a structured point cloud. The inputs \(X\) are mapped to outputs \(Y\) by the following:

\[Y_i = \sum_k w_k \cdot X_{n(i,k)} + b \quad\text{for}\; i \in 0,\ldots,|Y|-1,\]

where \(w_k\) are weights associated with the kernel, and \(n(i,k)\) is the neighborhood function described here.

Parameters

  • in_channels (int) – The number of channels in the input tensor.

  • out_channels (int) – The number of channels in the output tensor.

  • kernel_vectors (torch.ShortTensor) – A tensor of 3D offsets that define the shape of the kernel, see kernel creation.

  • jump (int, optional) – The difference between the input and output levels for the convolution. A non-zero value implies downsampling. Value must be positive and refer to a valid level of the structured point cloud. Default: 0.

  • bias (bool, optional) – If True, the convolution layer has a bias. Default: True.

forward(octrees, point_hierarchies, level, pyramids, exsum, input, **kwargs)
Parameters

  • octrees (torch.ByteTensor) – Packed octrees of shape \((\text{num_bytes})\). See octree.

  • point_hierarchies (torch.ShortTensor) – Packed point hierarchies of shape \((\text{num_points})\). See point_hierarchies.

  • level (int) – level at which the input features are associated to.

  • pyramids (torch.IntTensor) – Batched tensor containing point hierarchy structural information of shape \((\text{batch_size}, 2, \text{max_level}+2)\). See pyramids.

  • exsum (torch.IntTensor) – Tensor containing the Packed exclusive sum of the bit counts of individual octrees of shape \((\text{num_bytes} + \text{batch_size})\). See exsum.

  • input (torch.FloatTensor) – Packed input feature data of the octrees, of shape \((\text{total_num_inputs}, \text{in_channels})\), where total_num_inputs correspond to the number of nodes of the octrees at level, and in_channels is the input feature dimension (for instance 3 for RGB color).

Returns

  • Output of convolution. Number of outputs will correspond to level in the hierachy determined by jump.

  • the level associated to the output features.

Return type

(torch.FloatTensor, int)

reset_parameters()
training: bool
class kaolin.ops.spc.ConvTranspose3d(in_channels, out_channels, kernel_vectors, jump=0, bias=True)

Bases: torch.nn.modules.module.Module

Transposed convolution layer for a structured point cloud. The inputs \(X\) are mapped to outputs \(Y\) by the following:

\[Y_i = \sum_k w_k \cdot X_{n^T(i,k)} + b \quad\text{for}\; i \in 0,\ldots,|Y|-1,\]

where \(w_k\) are weights associated with the kernel, and \(n^T(i,k)\) is the transpose neighborhood function described here.

Parameters

  • in_channels (int) – The number of channels in the input tensor.

  • out_channels (int) – The number of channels in the output tensor.

  • kernel_vectors (torch.ShortTensor) – A tensor of 3D offsets that define the shape of the kernel. See kernel creation.

  • jump (int, optional) – The difference between the input and output levels for the convolution. Default: 0. A non-zero value implies upsampling. Value must be positive and refer to a valid level of the structured point cloud.

  • bias (bool, optional) – If True, the convolution layer has a bias. Default: True.

forward(octrees, point_hierarchies, level, pyramids, exsum, input, **kwargs)
Parameters

  • octrees (torch.ByteTensor) – Packed octrees of shape \((\text{num_bytes})\). See octree.

  • point_hierarchies (torch.ShortTensor) – Packed point hierarchies of shape \((\text{num_points})\). See point_hierarchies.

  • level (int) – level at which the input features are associated to.

  • pyramids (torch.IntTensor) – Batched tensor containing point hierarchy structural information of shape \((\text{batch_size}, 2, \text{max_level}+2)\). See pyramids.

  • exsum (torch.IntTensor) – Tensor containing the Packed exclusive sum of the bit counts of individual octrees of shape \((\text{num_bytes} + \text{batch_size})\). See exsum.

  • input (torch.FloatTensor) – Packed input feature data of the octrees, of shape \((\text{total_num_inputs}, \text{in_channels})\), where total_num_inputs correspond to the number of nodes of the octrees at level, and in_channels is the input feature dimension (for instance 3 for RGB color).

Returns

  • Output of transpose convolution. Number of outputs will correspond to level in the hierachy determined by jump.

  • the level associated to the output features.

Return type

(torch.FloatTensor, int)

reset_parameters()
training: bool
kaolin.ops.spc.bits_to_uint8(bool_t)

Convert uint8 ByteTensor to binary BoolTensor.

Parameters

bool_t (torch.BoolTensor) – Tensor to convert, of last dimension 8.

Returns

Converted tensor of same shape[:-1] and device than bool_t.

Return type

(torch.LongTensor)

Examples

>>> bool_t = torch.tensor(
... [[[1, 1, 0, 0, 0, 0, 0, 0],
...   [1, 0, 1, 0, 0, 0, 0, 0]],
...  [[0, 0, 0, 0, 1, 0, 0, 0],
...   [0, 1, 0, 0, 0, 0, 0, 0]]])
>>> bits_to_uint8(bool_t)
tensor([[ 3,  5],
        [16,  2]], dtype=torch.uint8)
kaolin.ops.spc.conv3d(octrees, point_hierarchies, level, pyramids, exsum, input, weight, kernel_vectors, jump=0, bias=None, **kwargs)

Convolution over a structured point cloud. The inputs \(X\) are mapped to outputs \(Y\) by the following:

\[Y_i = \sum_k w_k \cdot X_{n(i,k)} + b \quad\text{for}\; i \in 0,\ldots,|Y|-1,\]

where \(w_k\) are weights associated with the kernel, and \(n(i,k)\) is the neighborhood function described here.

Parameters

  • octrees (torch.ByteTensor) – Packed octrees of shape \((\text{num_bytes})\). See octree.

  • point_hierarchies (torch.ShortTensor) – Packed point hierarchies of shape \((\text{num_points})\). See point_hierarchies.

  • level (int) – level at which the input features are associated to.

  • pyramids (torch.IntTensor) – Batched tensor containing point hierarchy structural information of shape \((\text{batch_size}, 2, \text{max_level}+2)\). See pyramids.

  • exsum (torch.IntTensor) – Tensor containing the Packed exclusive sum of the bit counts of individual octrees of shape \((\text{num_bytes} + \text{batch_size})\). See exsum.

  • input (torch.FloatTensor) – Packed input feature data of the octrees, of shape \((\text{total_num_inputs}, \text{in_channels})\), where total_num_inputs correspond to the number of nodes of the octrees at level, and in_channels is the input feature dimension (for instance 3 for RGB color).

  • weight (torch.FloatTensor) – filter of shape \((\text{kernel_vectors.shape[0]}, \text{in_channels}, \text{self.out_channels})\).

  • kernel_vectors (torch.ShortTensor) – A tensor of 3D offsets that define the shape of the kernel. See kernel creation.

  • jump (int, optional) – The difference between the input and output levels for the convolution. A non-zero value implies downsampling. Value must be positive and refer to a valid level of the structured point cloud. Default: 0.

  • bias (torch.FloatTensor, optional) – optional bias tensor of shape \((\text{out_channel})\).

Returns

  • Output of convolution. Number of outputs will correspond to level in the hierachy determined by jump.

  • the level associated to the output features.

Return type

(torch.FloatTensor, int)

kaolin.ops.spc.conv_transpose3d(octrees, point_hierarchies, level, pyramids, exsum, input, weight, kernel_vectors, jump=0, bias=None, **kwargs)

Transposed convolution over a structured point cloud. The inputs \(X\) are mapped to outputs \(Y\) by the following:

\[Y_i = \sum_k w_k \cdot X_{n^T(i,k)} + b \quad\text{for}\; i \in 0,\ldots,|Y|-1,\]

where \(w_k\) are weights associated with the kernel, and \(n^T(i,k)\) is the transpose neighborhood function described here.

Parameters

  • octrees (torch.ByteTensor) – Packed octrees of shape \((\text{num_bytes})\). See octree.

  • point_hierarchies (torch.ShortTensor) – Packed point hierarchies of shape \((\text{num_points})\). See point_hierarchies.

  • level (int) – level at which the input features are associated to.

  • pyramids (torch.IntTensor) – Batched tensor containing point hierarchy structural information of shape \((\text{batch_size}, 2, \text{max_level}+2)\). See pyramids.

  • exsum (torch.IntTensor) – Tensor containing the Packed exclusive sum of the bit counts of individual octrees of shape \((\text{num_bytes} + \text{batch_size})\). See exsum.

  • input (torch.FloatTensor) – Packed input feature data of the octrees, of shape \((\text{total_num_inputs}, \text{in_channels})\), where total_num_inputs correspond to the number of nodes of the octrees at level, and in_channels is the input feature dimension (for instance 3 for RGB color).

  • weight (torch.FloatTensor) – filter of shape \((\text{kernel_vectors.shape[0]}, \text{in_channels}, \text{self.out_channels})\).

  • kernel_vectors (torch.ShortTensor) – A tensor of 3D offsets that define the shape of the kernel. See kernel creation.

  • jump (int, optional) – The difference between the input and output levels for the convolution. A non-zero value implies downsampling. Value must be positive and refer to a valid level of the structured point cloud. Default: 0.

  • bias (torch.FloatTensor, optional) – optional bias tensor of shape \((\text{out_channel})\).

kaolin.ops.spc.feature_grids_to_spc(feature_grids, masks=None)

Convert sparse feature grids to Structured Point Cloud.

Parameters

  • feature_grids (torch.Tensor) – The sparse 3D feature grids, of shape \((\text{batch_size}, \text{feature_dim}, X, Y, Z)\)

  • masks (optional, torch.BoolTensor) – The masks showing where are the features. Default: A feature is determined when not full or zeros.

Returns

a tuple containing:

  • The octree, of size \((\text{num_nodes})\)

  • The lengths of each octree, of size \((\text{batch_size})\)

  • The coalescent features, of same dtype than feature_grids, of shape \((\text{num_features}, \text{feature_dim})\).

Return type

(torch.ByteTensor, torch.IntTensor, torch.Tensor)

kaolin.ops.spc.generate_points(octrees, pyramids, exsum)

Generate the point data for a structured point cloud. Decode batched octree into batch of structured point hierarchies, and batch of book keeping pyramids.

Parameters

  • octrees (torch.ByteTensor) – Batched (packed) collection of octrees of shape \((\text{num_bytes})\).

  • pyramids (torch.IntTensor) – Batched tensor containing point hierarchy structural information of shape \((\text{batch_size}, 2, \text{max_level}+2)\)

  • exsum (torch.IntTensor) – Batched tensor containing the exclusive sum of the bit counts of individual octrees of shape \((k + \text{batch_size})\)

Returns

(torch.Tensor);

A tensor containing batched point hierachies derived from a batch of octrees

kaolin.ops.spc.morton_to_points(morton)

Convert morton codes to points.

Parameters

morton (torch.LongTensor) – The morton codes of quantized 3D points, of shape \((\text{num_points})\).

Returns

The points quantized coordinates, of shape \((\text{num_points}, 3)\).

Return type

(torch.ShortInt)

Examples

>>> inputs = torch.tensor([0, 1, 8, 9, 2], device='cuda')
>>> morton_to_points(inputs)
tensor([[0, 0, 0],
        [0, 0, 1],
        [0, 0, 2],
        [0, 0, 3],
        [0, 1, 0]], device='cuda:0', dtype=torch.int16)
kaolin.ops.spc.points_to_coeffs(x, points)

Calculates the coefficients for trilinear interpolation.

To interpolate with the coefficients, do: torch.sum(features * coeffs, dim=-1) with features of shape \((\text{num_points}, 8)\)

Parameters

  • x (torch.FloatTensor) – Floating point 3D points, of shape \((\text{num_points}, 3)\).

  • points (torch.ShortTensor) – Quantized 3D points (the 0th bit of the voxel x is in), of shape \((\text{num_points}, 3)\).

Returns

The trilinear interpolation coefficients,

of shape \((\text{num_points}, 8)\).

Return type

(torch.FloatTensor)

kaolin.ops.spc.points_to_corners(points)

Calculates the corners of the points assuming each point is the 0th bit corner.

Parameters

points (torch.ShortTensor) – Quantized 3D points, of shape \((\text{num_points}, 3)\).

Returns

Quantized 3D new points,

of shape \((\text{num_points}, 8, 3)\).

Return type

(torch.ShortTensor)

Examples

>>> inputs = torch.tensor([
...     [0, 0, 0],
...     [0, 2, 0]], device='cuda', dtype=torch.int16)
>>> points_to_corners(inputs)
tensor([[[0, 0, 0],
         [0, 0, 1],
         [0, 1, 0],
         [0, 1, 1],
         [1, 0, 0],
         [1, 0, 1],
         [1, 1, 0],
         [1, 1, 1]],

        [[0, 2, 0],
         [0, 2, 1],
         [0, 3, 0],
         [0, 3, 1],
         [1, 2, 0],
         [1, 2, 1],
         [1, 3, 0],
         [1, 3, 1]]], device='cuda:0', dtype=torch.int16)
kaolin.ops.spc.points_to_morton(points)

Convert (quantized) 3D points to morton codes.

Parameters

points (torch.ShortTensor) – Quantized 3D points. This is not exactly like SPC points hierarchies as this is only the data for a specific level, of shape \((\text{num_points}, 3)\).

Returns

The morton code of the points, of shape \((\text{num_points})\)

Return type

(torch.LongTensor)

Examples

>>> inputs = torch.tensor([
...     [0, 0, 0],
...     [0, 0, 1],
...     [0, 0, 2],
...     [0, 0, 3],
...     [0, 1, 0]], device='cuda', dtype=torch.int16)
>>> points_to_morton(inputs)
tensor([0, 1, 8, 9, 2], device='cuda:0')
kaolin.ops.spc.quantize_points(x, level)

Quantize [-1, 1] float coordinates in to [0, (2^level)-1] integer coords.

If a point is out of the range [-1, 1] it will be clipped to it.

Parameters

  • x (torch.FloatTensor) – floating point coordinates, must but of last dimension 3.

  • level (int) – Level of the grid

Returns

(torch.ShortTensor): Quantized 3D points, of same shape than x.

kaolin.ops.spc.scan_octrees(octrees, lengths)

Scan batch of octrees tensor.

Scanning refers to processing the octrees to extract auxiliary information.

There are two steps. First, a list is formed containing the number of set bits in each octree node/byte. Second, the exclusive sum of this list is taken.

Parameters

  • octrees (torch.ByteTensor) – Batched packed collection of octrees of shape \((\text{num_node})\).

  • lengths (torch.IntTensor) – The number of byte per octree. of shape \((\text{batch_size})\).

Returns

  • An int containing the depth of the octrees.

  • A tensor containing structural information about the batch of structured point cloud hierarchies, see pyramids example.

  • A tensor containing the exclusive sum of the bit counts of each byte of the individual octrees within the batched input octrees tensor, see exsum.

Return type

(int, torch.IntTensor, torch.IntTensor)

Note

The returned tensor of exclusive sums is padded with an extra element for each item in the batch.

kaolin.ops.spc.to_dense(point_hierarchies, pyramids, input, level=- 1, **kwargs)

Convert batched structured point cloud to a batched dense feature grids.

The size of the input should correspond to level \(l\) within the structured point cloud hierarchy. A dense voxel grid of size \((\text{batch_size}, 2^l, 2^l, 2^l, \text{input_channels})\) is returned where (for a particular batch):

\[Y_{P_i} = X_i \quad\text{for}\; i \in 0,\ldots,|X|-1,\]

where \(P_i\) is used as a 3D index for dense array \(Y\), and \(X_i\) is the input feature corresponding to to point \(P_i\). Locations in \(Y\) without a correspondense in \(X\) are set to zero.

Parameters

  • point_hierarchies (torch.ShortTensor) – Packed collection of point hierarchies, of shape \((\text{num_points})\). See point_hierarchies for a detailed description.

  • pyramids (torch.IntTensor) – Batched tensor containing point hierarchy structural information of shape \((\text{batch_size}, 2, \text{max_level}+2)\). See pyramids for a detailed description.

  • input (torch.FloatTensor) – Batched tensor of input feature data, of shape \((\text{num_inputs}, \text{feature_dim})\). The number of inputs, \(\text{num_inputs}\), must correspond to number of points in the batched point hierarchy at level.

  • level (int) – The level at which the octree points are converted to feature grids.

Returns

The feature grids, of shape \((\text{batch_size}, \text{feature_dim}, 8^\text{level}, 8^\text{level}, 8^\text{level})\).

Return type

(torch.FloatTensor)

kaolin.ops.spc.uint8_bits_sum(uint8_t)

Compute the bits sums for each byte in ByteTensor.

Parameters

uint8_t (torch.ByteTensor) – Tensor to process.

Returns

Output of same shape and device than uint8_t.

Return type

(torch.LongTensor)

Examples

>>> uint8_t = torch.ByteTensor([[255, 2], [3, 40]])
>>> uint8_bits_sum(uint8_t)
tensor([[8, 1],
        [2, 2]])
kaolin.ops.spc.uint8_to_bits(uint8_t)

Convert uint8 ByteTensor to binary BoolTensor.

Parameters

uint8_t (torch.ByteTensor) – Tensor to convert.

Returns

Converted tensor of same shape + last dimension 8 and device than uint8_t.

Return type

(BoolTensor)

Examples

>>> uint8_t = torch.ByteTensor([[3, 5], [16, 2]])
>>> uint8_to_bits(uint8_t)
tensor([[[ True,  True, False, False, False, False, False, False],
         [ True, False,  True, False, False, False, False, False]],

        [[False, False, False, False,  True, False, False, False],
         [False,  True, False, False, False, False, False, False]]])
kaolin.ops.spc.unbatched_points_to_octree(points, level, sorted=False)

Convert (quantized) 3D points to an octree.

This function assumes that the points are all in the same frame of reference of [0, 2^level]. Note that SPC.points does not satisfy this constraint.

Parameters

  • points (torch.ShortTensor) – The Quantized 3d points. This is not exactly like SPC points hierarchies as this is only the data for a specific level.

  • level (int) – Max level of octree, and the level of the points.

  • sorted (bool) – True if the points are unique and sorted in morton order.

Returns

the generated octree,

of shape \((2^\text{level}, 2^\text{level}, 2^\text{level})\).

Return type

(torch.ByteTensor)

kaolin.ops.spc.unbatched_query(octree, point_hierarchy, pyramid, exsum, query_points, level)

Query point indices from the octree.

Given a point hierarchy, this function will efficiently find the corresponding indices of the points in the points tensor. For each input in query_points, returns a index to the points tensor.

Parameters

  • octree (torch.ByteTensor) – The octree, of shape \((\text{num_bytes})\).

  • point_hierarchy (torch.ShortTensor) – The points hierarchy, of shape \((\text{num_points}, 3)\). See point_hierarchies: for more details.

  • pyramid (torch.IntTensor) – The pyramid info of the point hierarchy, of shape \((2, \text{max_level} + 2)\). See pyramids: for more details.

  • exsum (torch.IntTensor) – The exclusive sum of the octree bytes, of shape \((\text{num_bytes} + 1)\). See pyramids: for more details.

  • query_points (torch.ShortTensor) – A collection of query indices, of shape \((\text{num_query}, 3)\).

  • level (int) – The level of the octree to query from.